0xf2 - Partir un arreglo grande en 2

Tenemos un arreglo de enteros. Queremos partirlo en dos arreglos de tal manera que:

• La suma de los elementos en el lado izquierdo sea positiva;
• La suma de los elementos en el lado derecho sea negativa.

No está permitido reordenar o cambiar los elementos del arreglo.

Por ejemplo, supongamos que tenemos el arreglo A = [5, 1, -2, 3, -4]. Ésta es un manera de partirlo:

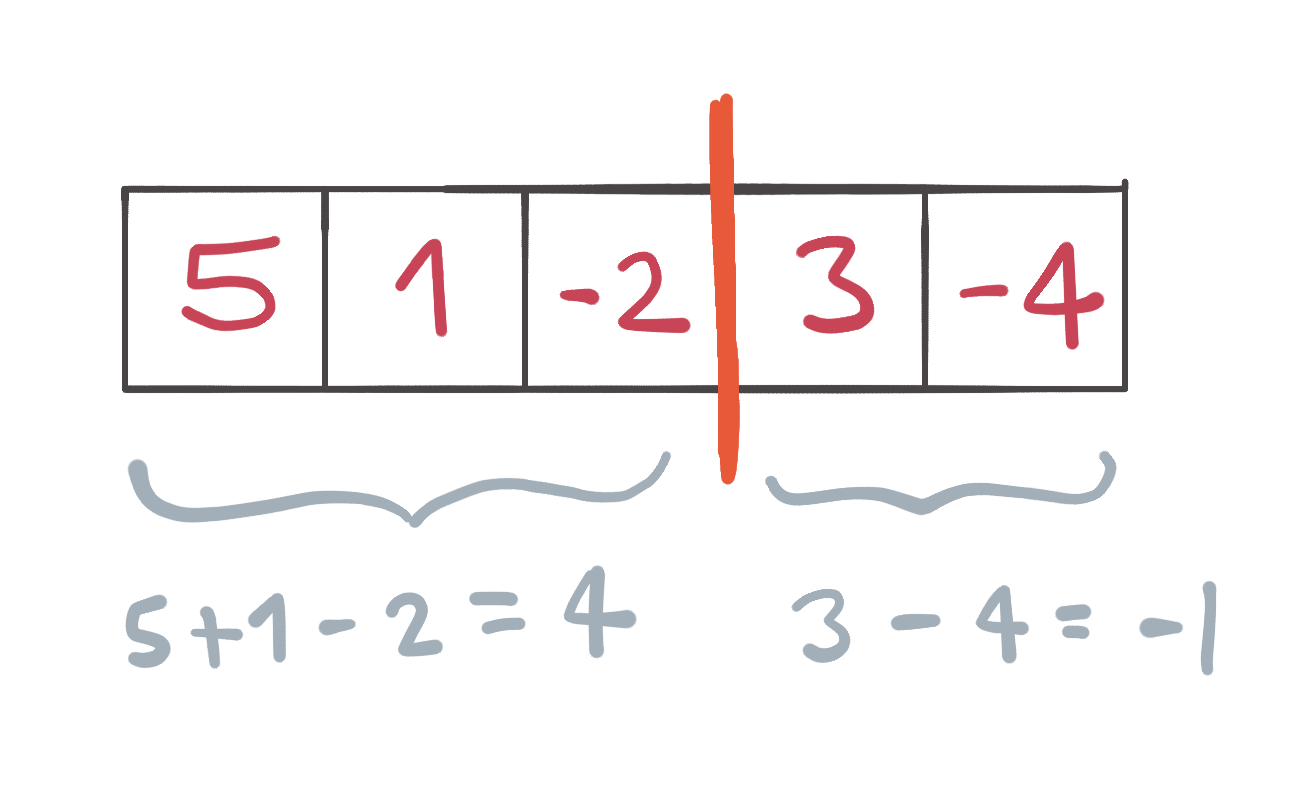
Esta es una solución válida porque la suma del lado izquierdo es positiva (5 + 1 - 2 = 4 > 0) y la suma del lado derecho es negativa (3 - 4 = -1 < 0).

A veces, es posible encontrar varias soluciones válidas. Si esto sucede, preferimos la solución que tenga el lado izquierdo más pequeño. Ésta es la mejor solución para nuestro ejemplo:

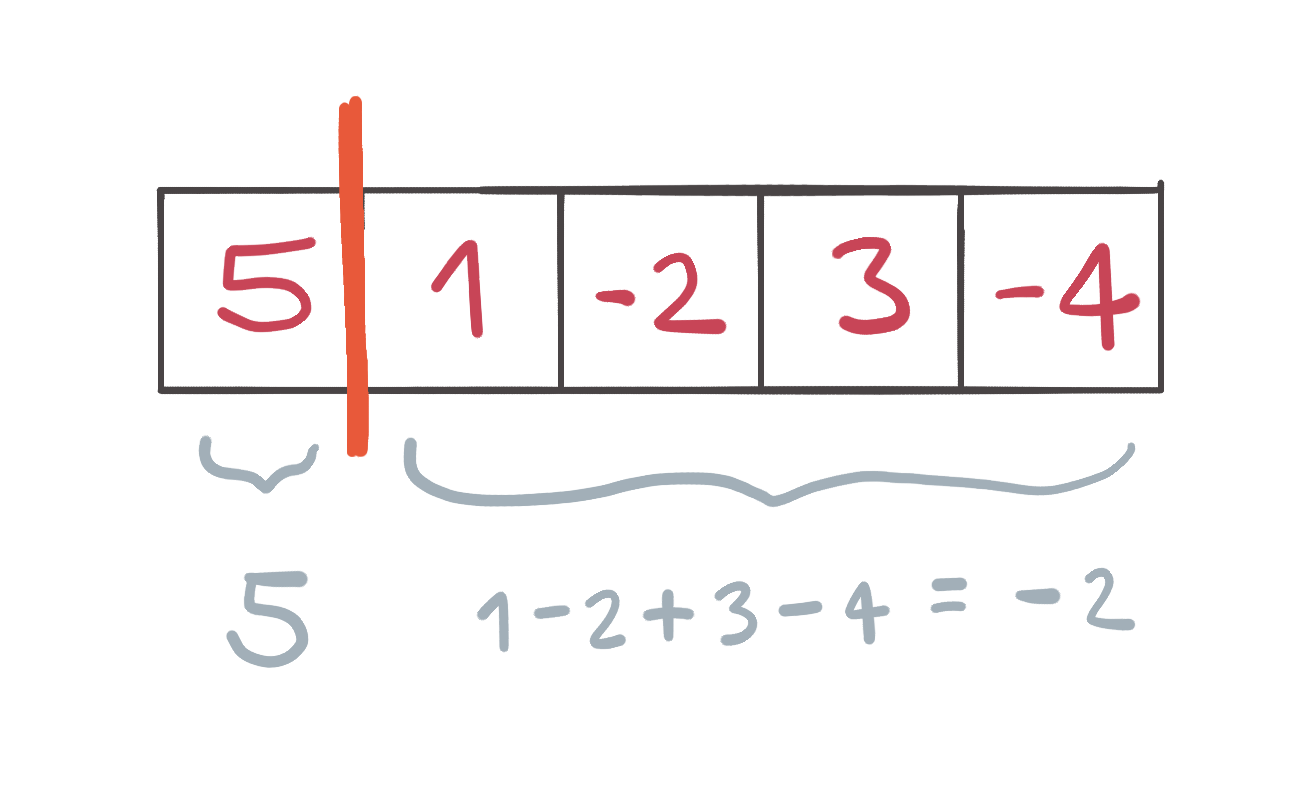
Escribe un programa que dado un arreglo encuentra la mejor solución, si existe.

Entrada

La entrada contiene 2 líneas:

• La primera línea contiene N, el número de elementos en el arreglo.
• La segunda línea contiene N enteros Ai para 0 ≤ i < N, los elementos del arreglo. Estos números están separados por espacios. Está garantizado que Ai satisface -10³ ≤ Ai ≤ 10³.

Salida

La salida debe tener exactamente una línea:

• Si hay solución, la línea debe contener el índice (basado en 0) del primer elemento del lado derecho.
• Si no hay solución, la línea debe contener la palabra Impossible (Atención: ¡Está en inglés y se escribe con doble s!);

Si hay varias soluciones, escoge la solución en la que el lado izquierdo sea más pequeño.

Entrada de ejemplo #1

5
5 1 -2 3 -4

Salida de ejemplo #1

1

Explicación del ejemplo #1

Este es el ejemplo del dibujo. La mejor solución es [5 | 1 -2 3 4]. El índice del primer elemento del lado derecho es 1, por eso la salida es 1.

Entrada de ejemplo #2

6
-1 2 3 4 5 -1

Salida de ejemplo #2

5

Explicación del ejemplo #2

La única solución es [-1 2 3 4 5 | -1] (cualquier otra partición hace que la suma del lado derecho sea positiva y necesitamos que sea negativa). El problema nos pide imprimir el índice (basado en 0) del primer elemento del lado derecho. En este caso, el índice es 5.

Entrada de ejemplo #3

5
-1 2 3 4 -5

Salida de ejemplo #3

3

Explicación del ejemplo #3

Hay 2 soluciones: [-1 2 3 | 4 -5] y [-1 2 3 4 | -5]. Escogemos la primera porque su lado izquierdo es más pequeño. El índice del primer elemento del lado derecho en esta solución es 3.

Entrada de ejemplo #4

5
-1 -2 3 -4 -5

Salida de ejemplo #4

Impossible

Explicación del ejemplo #4

Ningúna partición hace que la suma del lado izquierdo sea positiva, por lo tanto no hay solución. Por ejemplo, en la partición [-1 -2 | 3 -4 -5] la suma del lado izquierdo es -3, que no es válido. Lo más cercano a una solución es [-1 -2 3 | -4 -5]. En este caso la suma del lado izquierdo es 0 (pero 0 no es positivo).

Restricciones

Está garantizado que:

• En aproximadamente 70% de los casos, 2 <= N <= 1000.
• En el resto de los casos, 2 <= N <= 500,000.

Envía tu solución