0xe1 - Cuadrado mágico

Tenemos una matriz cuadrada de N x N números enteros.

Decimos que la matriz es un cuadrado mágico si la suma de sus filas, columnas y diagonales es siempre la misma.

Por ejemplo, esta matriz es un cuadrado mágico porque la suma de todas sus filas, columnas y diagonales siempre es 6:

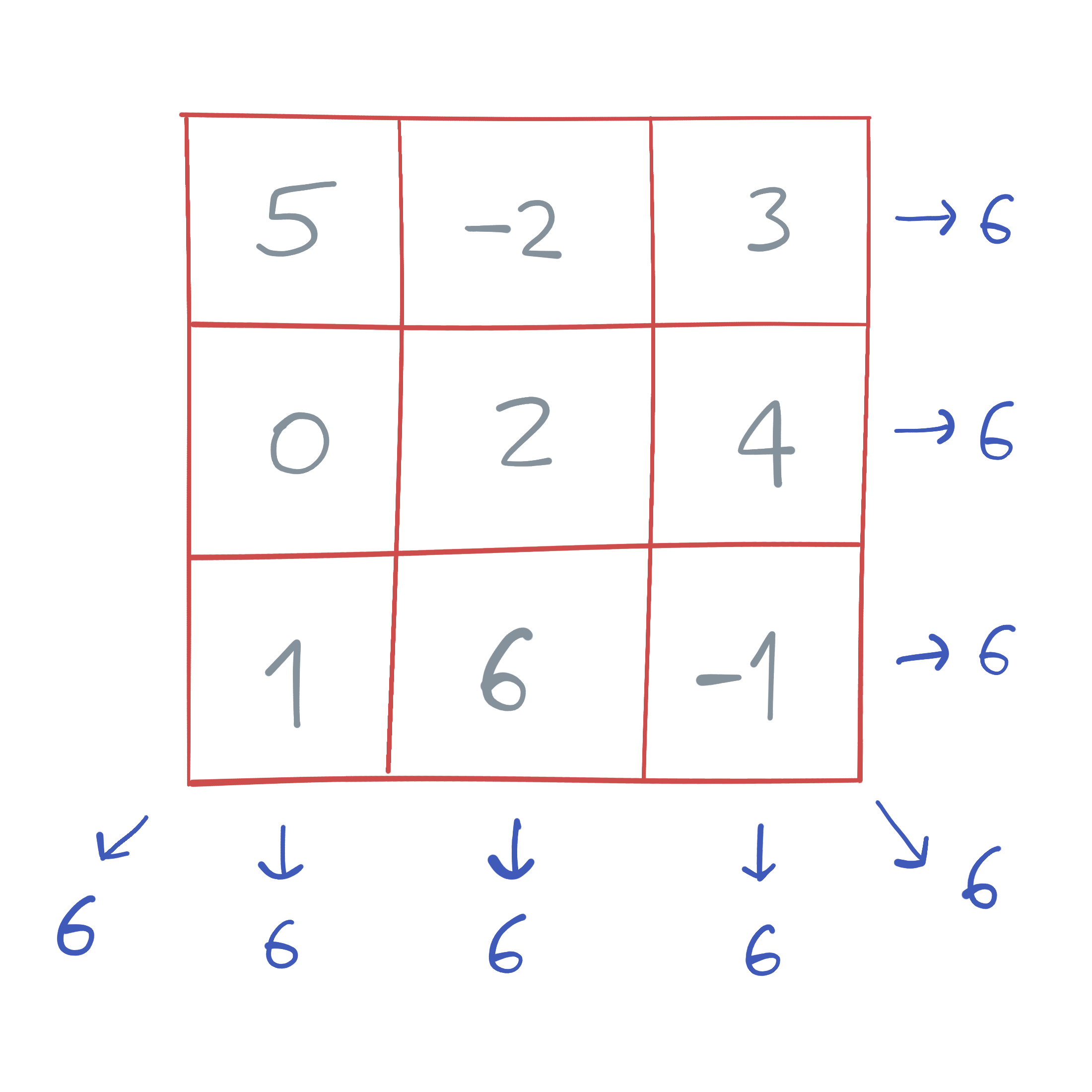
Escribe un programa que lee una matriz y determina si la matriz es un cuadrádo mágico o no.

Entrada

La entrada contiene N+1 líneas:

• La primera línea contiene N, el número de filas y columnas de la matriz.
• Luego vienen N líneas cada una con N enteros separados por espacios, los elementos de la matriz. Está garantizado que cualquier elemento Ai,j de la matriz satisface -1000 ≤ Ai,j ≤ 1000.

Salida

La salida debe tener exactamente una línea:

• Si la matriz es una cuadrado mágico, la salida debe ser Yes;
• Si la matriz no es un cuadrado mágico a salida debe ser No.

Entrada de ejemplo 1

3
5 -2 3
0 2 4
1 6 -1

Salida de ejemplo 1

Yes

Explicación del ejemplo 1

Este es el ejemplo de la imagen.

Entrada de ejemplo 2

3
2 3 4
5 3 1
2 3 4

Salida de ejemplo 2

Yes

Explicación del ejemplo 2

Esta matriz es un cuadrado mágico porque la suma de sus filas, columnas y diagonales siempre es 9.

Entrada de ejemplo 3

4
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1

Salida de ejemplo 3

Yes

Explicación del ejemplo 3

Cuando todos los elementos son iguales la matriz siempre es un cuadrado mágico.

Entrada de ejemplo 4

3
1 0 0
0 0 1
0 1 0

Salida de ejemplo 4

No

Explicación del ejemplo 4

Esta matriz es casi un cuadrado mágico, pero la suma de una de sus diagonales es cero y todas las demás son 1.

Restricciones

• Está garantizado que 2 ≤ N ≤ 100.

Envía tu solución