0xcf - Mirando al horizonte

En una calle hay N edificios de varias alturas numerados de 0 a N-1 de izquierda a derecha:

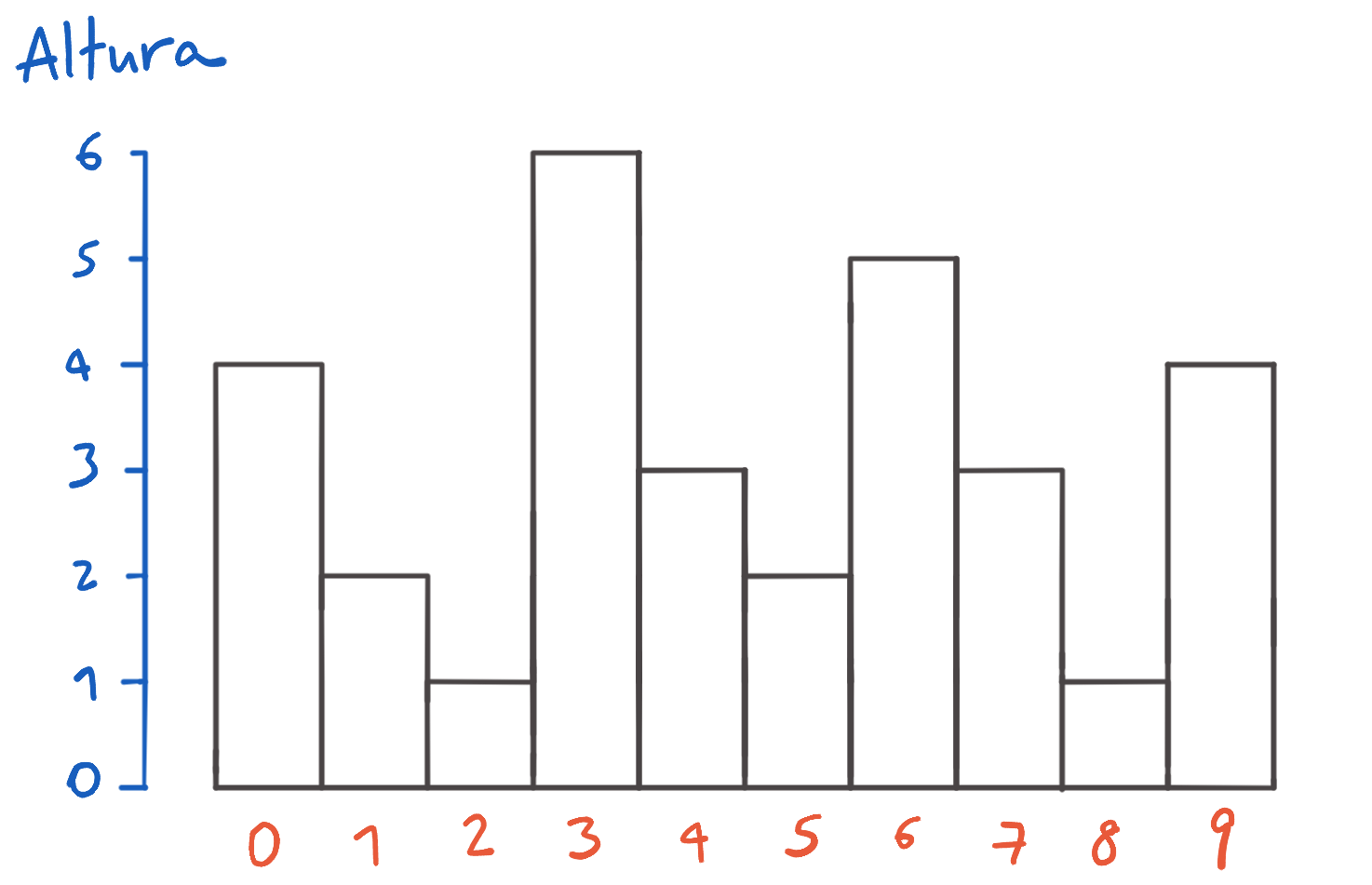
Una persona se sube al techo de cada edificio y mira en una línea recta paralela al suelo en la dirección en la que aumentan los números de los edificios (hacia la derecha en el diagrama). A veces, la persona logra ver el horizonte en la distancia, pero a veces no porque un edificio más alto bloquea la vista.

Por ejemplo, desde el edificio 0 (que tiene altura 4) no se ve el horizonte porque el edificio 3 (que tiene altura 6) bloquea la vista. Similarmente, desde el edificio 4 tampoco se ve el horizonte porque el edificio 6 bloquea la vista. Desde los edificios 3, 6 y 9, en cambio, sí se puede ver el horizonte en la distancia porque ningún otro edificio bloquea la vista:

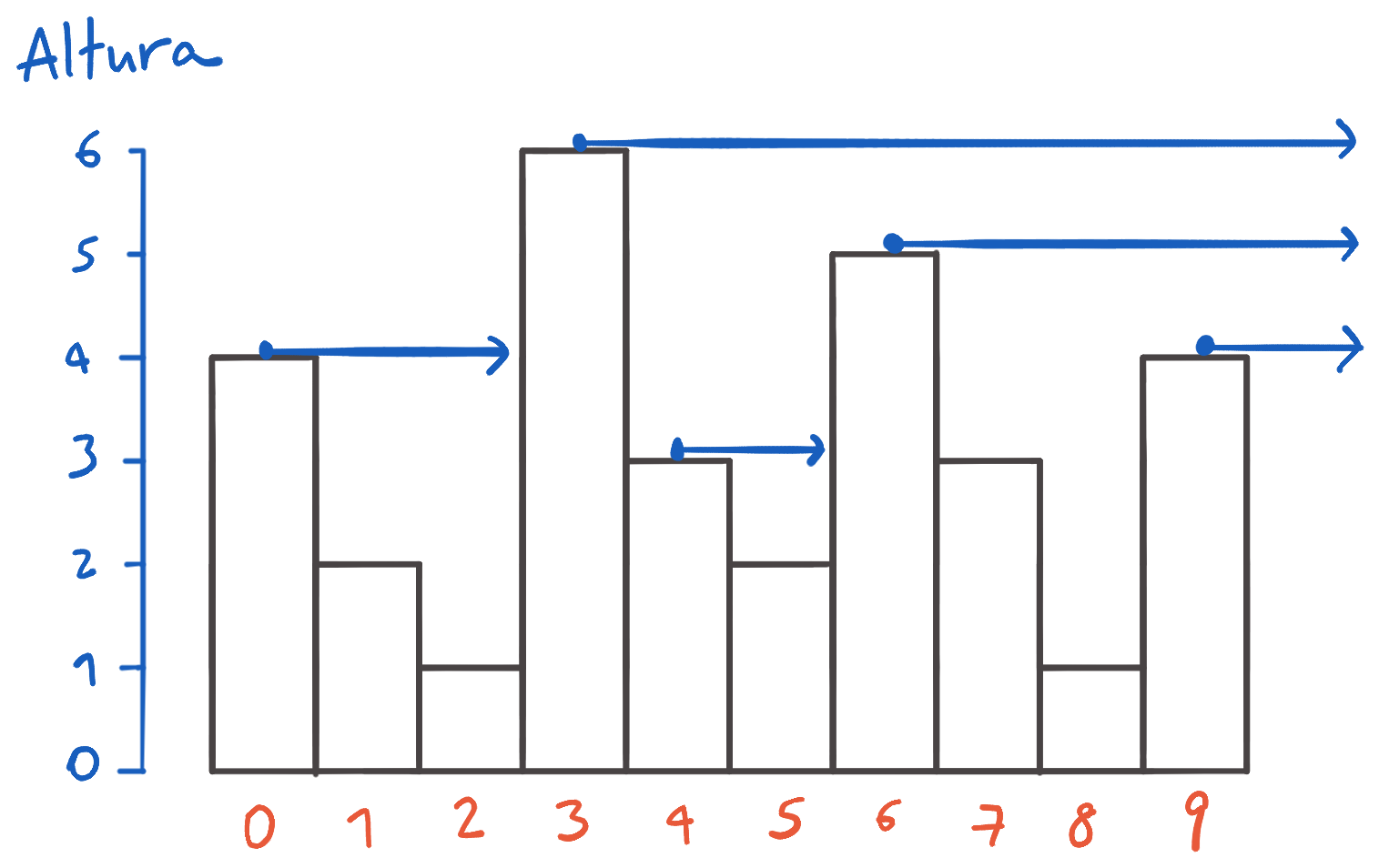
Escribe un programa que calcula, para cada edificio, si es posible ver el horizonte o no. Si no es posible, tu programa debe determinar la altura del edificio que está bloqueando la vista.

Entrada

El archivo de entrada contiene varios casos de prueba. En la primera línea hay un número C, el número de casos.

Luego siguen C casos, cada uno compuesto de 2 líneas:

• La primera línea tiene N, el número de edificios.
• La segunda línea tiene N números enteros: la altura ai del edificio i para todo 0 ≤ i < N. Está garantizado que ai satisface 0 ≤ ai ≤ 10⁹.

Salida

Para cada caso, la salida debe tener una línea en el formato Case #x: v0 v1 ... vn-1, donde x es el número de caso (empezando en 1) y vi es la altura del edificio que bloquea la vista al mirar al horizonte desde el techo del edificio i, ó -1 si ningún edificio bloquea la vista.

Entrada de ejemplo

3
10
4 2 1 6 3 2 5 3 1 4
3
1 1 2
6
3 3 2 2 1 1

Salida de ejemplo

Case #1: 6 6 6 -1 5 5 -1 4 4 -1
Case #2: 2 2 -1
Case #3: -1 -1 -1 -1 -1 -1

Restricciones

Está garantizado que:

• En 50% de los casos, 1 <= N <= 100.
• En el otro 50% de los casos, 1 <= N <= 500000.

Envía tu solución