0xcb - Contar maneras de formar una cantidad con monedas

En Estados Unidos hay monedas de 1, 5, 10 y 25 centavos. Usando sólo monedas de estas denominaciones, es posible encontrar varias maneras diferentes de formar una cantidad de dinero específica.

Por ejemplo, aquí hay algunas de las maneras de formar 1 dólar (o lo que es lo mismo, 100 centavos):

• 100 monedas de 1 centavo = 1 dólar:

• 10 monedas de 5 centavos + 5 monedas de 10 centavos = 1 dólar;

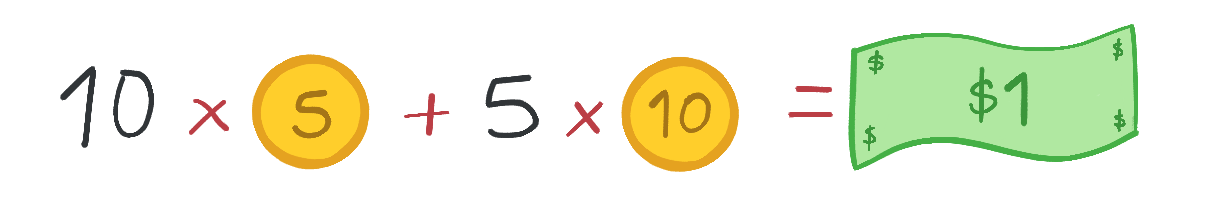
• 4 monedas de 25 centavos = 1 dólar;

• 5 monedas de 1 centavo + 2 monedas de 5 centavos + 1 moneda de 10 centavos + 3 monedas de 25 centavos = 1 dólar.

Estos son sólo algunos ejemplos porque la lista es bastante larga. De hecho, existen 242 maneras diferentes de formar un dólar usando sólo monedas de estas denominaciones (si tienes curiosidad, aquí está la lista completa).

Escribe un programa que recibe N denominaciones de monedas diferentes y M consultas, cada una con un valor de dinero específico (en centavos). Para cada consulta, encuentra el número de maneras en las que se puede formar esa cantidad de dinero usando sólo monedas de las denominaciones dadas.

Es válido asumir que se cuenta con una cantidad infinita de monedas de todas las denominaciones (es decir, nunca se te van acabar las monedas de ninguna denominación).

Dos maneras son consideradas iguales si y sólo si usan el mismo número de monedas de cada denominación. En otras palabras, el orden de las monedas no importa (por ejemplo, "9 monedas de 10 centavos + 2 monedas de 5 centavos" es exactamente lo mismo a "2 monedas de 5 centavos + 9 monedas de 10 centavos").

Entrada

La entrada contiene varias líneas:

• La primera línea contiene N, el número de denominaciones de monedas que podemos usar. Está garantizado que 0 ≤ N ≤ 500.
• La segunda línea contiene N enteros Di para 0 ≤ i < N, todas las denominaciones (en centavos). Estos números están separados por espacios.
  • Está garantizado que cada Di satisface 1 ≤ Di ≤ 109.
  • Está garantizado que todas las denominaciones son diferentes (es decir, no hay duplicados en esta lista).
• La tercera línea contiene M, el número de consultas. Está garantizado que 0 ≤ M ≤ 20,000.
• Luego vienen M líneas cada una con un consulta descrita por un entero S, la cantidad de centavos que queremos formar. Está garantizado que todas las consultas cumplen 0 ≤ S ≤ 10,000.

Salida

La salida debe tener exactamente M líneas (una por consulta).

Para cada consulta, escribe el número de maneras en que se pueden formar S centavos usando sólo monedas de las denominaciones dadas.

Cómo este número puede ser demasiado grande, imprímelo módulo 1000000007 para que el resultado quepa en un entero con signo de 32 bits.

Entrada de ejemplo 1

4
1 5 10 25
5
100
4
5
10
0

Salida de ejemplo 1

242
1
2
4
1

Explicación del ejemplo 1

• La primera línea nos dice que hay N = 4 denominaciones diferentes.
• La segunda línea nos dice que estas denominaciones son monedas de 1, 5, 10 y 25 centavos.
• La tercera línea nos dice que siguen M = 5 consultas.
• La primera consulta es S = 100 centavos (1 dólar). Este es el ejemplo explicado más arriba y como ya se dijo hay 242 maneras diferentes de formar un dólar con estas denominaciones.
• La segunda consulta es S = 4 centavos. Sólo hay una manera de formar 4 centavos con estas denominaciones: usar 4 monedas de 1 centavo.
• La tercera consulta es S = 5 centavos. Ahora hay 2 maneras de formar 5 centavos:
  • 5 monedas de 1 centavo;
  • 1 moneda de 5 centavos.
• La cuarta consulta es S = 10 centavos. Estas son las 4 maneras de formar 10 centavos:
  • 10 monedas de 1 centavo;
  • 5 monedas de 1 centavo + una moneda de 5 centavos;
  • 2 monedas de 5 centavos;
  • 1 moneda de 10 centavos.
• La quinta y última consulta es S = 0 centavos. Hay exactamente una manera de formar 0 centavos: no agarrar ninguna moneda.

Entrada de ejemplo 2

6
2 4 6 8 10 12
2
17
10000

Salida de ejemplo 2

0
243563893

Explicación del ejemplo 2

• Ahora tenemos monedas de 2, 4, 6, 8, 10 y 12 centavos.
• La primera consulta es S = 17 centavos. Cómo todas las denominaciones son números pares, es imposible formar una cantidad impar. Por lo tanto la respuesta para esta consulta es 0.
• La segunda consulta es S = 10000 centavos. Realmente hay 36550243819743 maneras de formar esta cantidad, pero el enunciado nos pide encontrar el número de maneras módulo 1000000007. Todos sabemos que 36550243819743 módulo 1000000007 es 243563893, por eso la salida es 243563893.

Entrada de ejemplo 3

1
1
5
0
1
20
300
4000

Salida de ejemplo 3

1
1
1
1
1

Explicación del ejemplo 3

Cuando sólo tenemos monedas de un centavo, la salida siempre es 1 porque podemos formar cualquier cantidad pero sólo de una única una manera.

Entrada de ejemplo 4

1
3
6
3
4
5
6
7
8

Salida de ejemplo 4

1
0
0
1
0
0

Explicación del ejemplo 4

Cuando sólo tenemos monedas de una denominación (en este caso monedas de 3 centavos), sólo podemos formar valores que son múltiplos de esa denominación (y de sólo una manera). Por eso la salida es 1 para los múltiplos de 3 (como 3 y 6) y 0 para los demás valores (como 4 y 5).

Envía tu solución