0xca - Contar cuantas veces aparece X en un subarreglo

Tenemos un arreglo A con muchos elementos. Dado un entero X y dos índices L y R, queremos responder esta pregunta: ¿Cuántas veces aparece X en el subarreglo de A que empieza en el índice L y termina en el índice R?

Por ejemplo, supongamos que nos dan este arreglo (los números en la parte superior son índices):

A = [2, 1, 1, -5, 1, 3, 1]

Si nos dan L = 2, R = 5 y X = 1, entonces la respuesta es 2, porque:

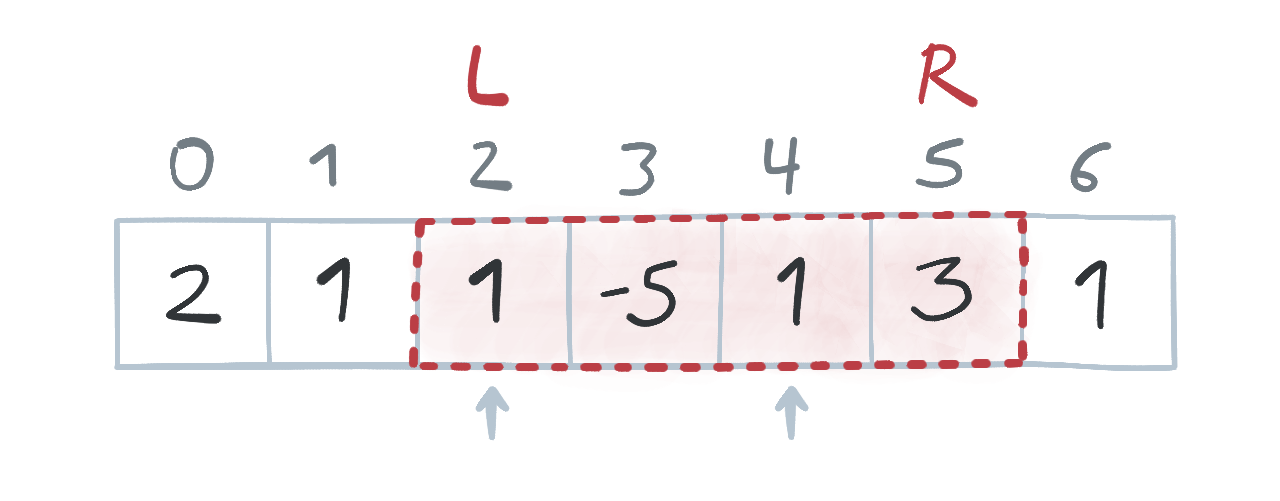
El subarreglo que empieza en el índice L = 2 y termina en el índice R = 5 es [1, -5, 1, 3] (la zona resaltada en rojo en la próxima imagen).
En este subarreglo el valor X = 1 aparece 2 veces (las dos casillas señaladas con flechas).

Imagen con L = 2, R = 5 y X = 1

Escribe un programa que recibe el arreglo A y procesa rápidamente varias consultas, cada una con valores diferentes de L, R y X.

Entrada

La entrada contiene varias líneas:

La primera línea contiene N, el número de elementos en el arreglo.
La segunda línea contiene N enteros A_i para 0 ≤ i < N, los elementos del arreglo. Estos números están separados por espacios. Está garantizado que A_i satisface -10⁹ ≤ A_i ≤ 10⁹.
La tercera línea contiene C, el número de consultas.
Luego vienen C líneas, cada una con un consulta descrita por tres enteros L, R y X, separados por espacios. Está garantizado que 0 ≤ L ≤ R < N; es decir, tanto L cómo R son índices válidos del arreglo (comenzando en 0) y L nunca está a la derecha de R. También está garantizado que -10⁹ ≤ X ≤ 10⁹.

Salida

La salida debe tener exactamente C líneas (una por consulta).

Para cada consulta, escribe cuántas veces aparece X en el subarreglo de A que empieza en el índice L y termina en el índice R (ambos incluídos).

Entrada de ejemplo

7
2 1 1 -5 1 3 1
5
2 5 1
2 5 -5
2 5 4
0 6 1
5 5 3

Salida de ejemplo

Explicación del ejemplo

La entrada nos da el mismo arreglo de la imagen más arriba, A = [2, 1, 1, -5, 1, 3, 1], y 5 consultas:

La primera consulta es el ejemplo explicado en la imagen más arriba (L = 2, R = 5 y X = 1). La respuesta es 2 porque X = 1 aparece dos veces en [1, -5, 1, 3].
La segunda consulta es L = 2, R = 5 y X = -5. La respuesta es 1 porque X = -5 aparece sólo una vez en [1, -5, 1, 3].
La tercera consulta es L = 2, R = 5 y X = 4. La respuesta es 0 porque 4 no aparece ni una vez en [1, -5, 1, 3].
La cuarta consulta es L = 0, R = 6 (el arreglo completo) y X = -1. La respuesta es 4 porque hay cuatro unos en todo el arreglo.
La quinta consulta es L = 5, R = 5 (un subarreglo de un sólo elemento) y X = 3. La respuesta es 1 porque por casualidad A[5] = 3 = X.

Restricciones

Está garantizado que 1 ≤ N ≤ 100,000 y 1 ≤ C ≤ 100,000.