0xa6 - Submatriz de suma máxima en una matriz no muy grande
Tenemos una matriz de R x C números enteros. Los números pueden ser negativos, positivos o cero:

Una submatriz es un bloque rectangular de elementos tomados de la matriz original. Decimos que la suma de una submatriz es la suma de todos los elementos dentro de ella. Por ejemplo, aquí hay una submatriz de suma 9:
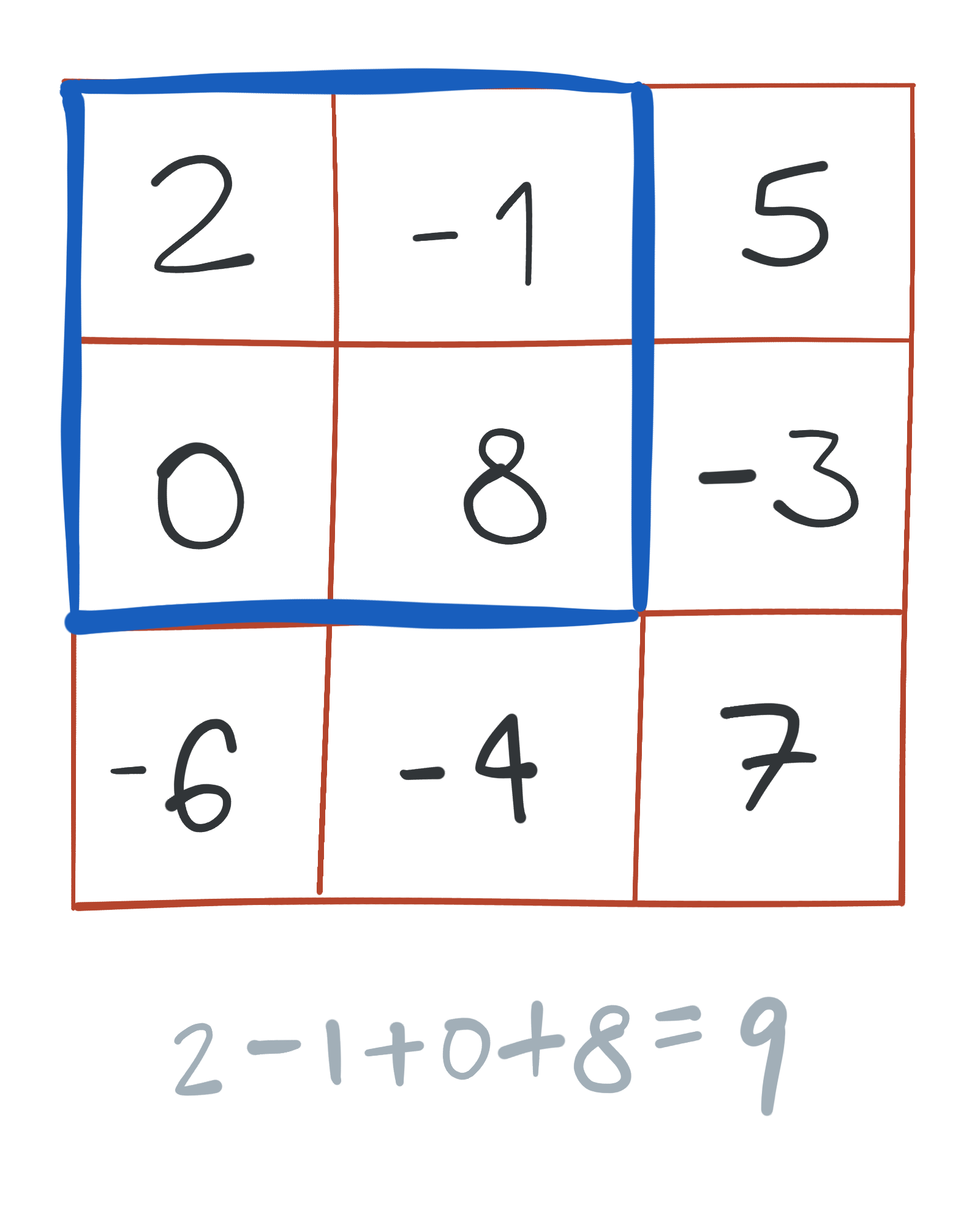
Diferentes submatrices pueden tener diferentes sumas. Por ejemplo, aquí hay una submatriz cuya suma es 12:
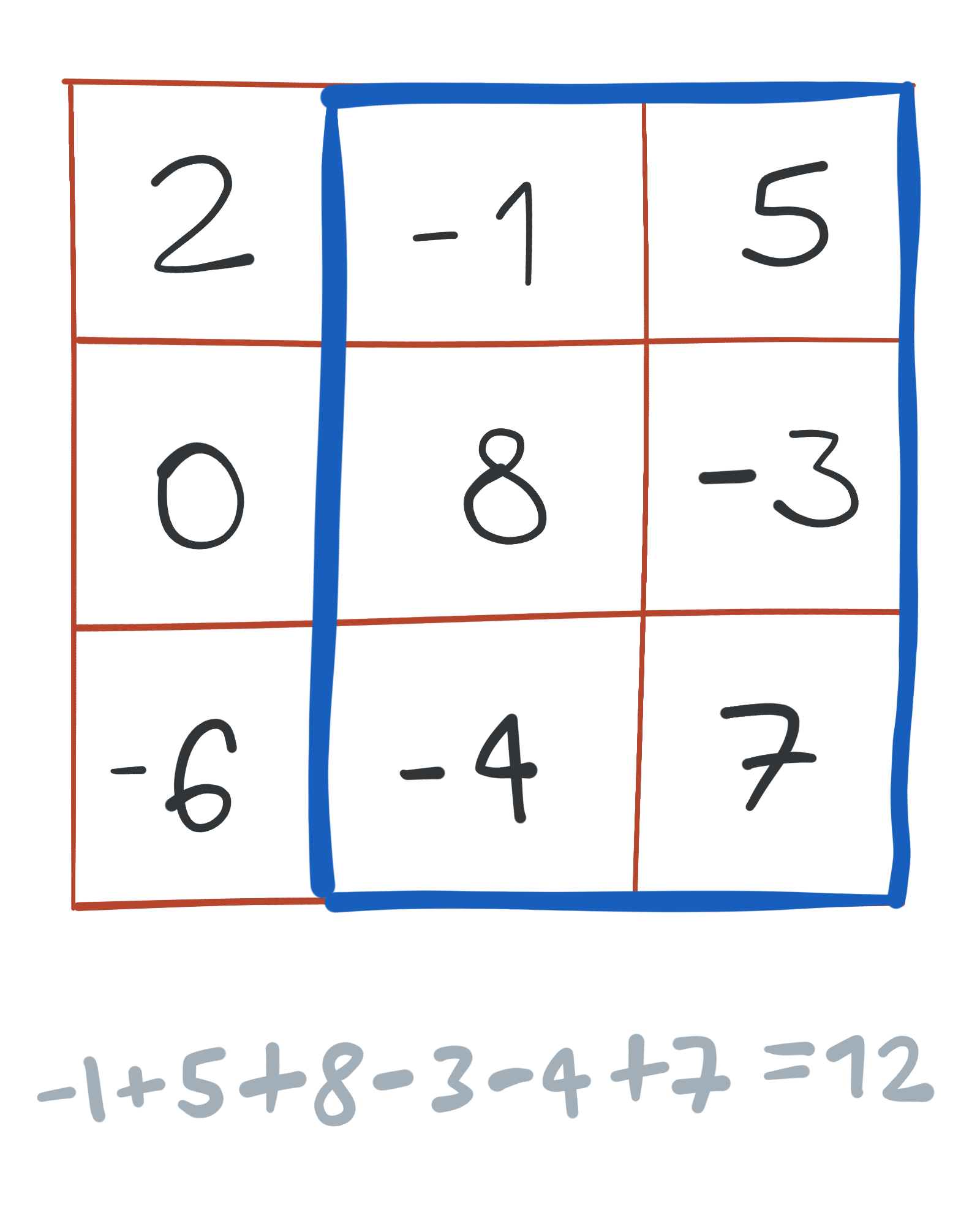
En este problema nos interesa encontrar la submatriz cuya suma sea máxima. La submatriz anterior cuya suma es 12 es la mejor posible en este ejemplo.
Escribe un programa que lee una matriz y calcula la máxima suma entre todas las posibles submatrices. Sólo debes considerar submatrices que contienen por lo menos un elemento (es decir, no es valido considerar una submatriz vacía).
Entrada
La entrada contiene varias líneas:
- La primera línea contiene dos números
RyCseparados por un espacio.RyCson el número de filas (rows) y el número de columnas (columns) en la matriz, respectivamente. - Luego vienen
Rlíneas cada una conCenteros separados por espacios, los elementos de la matriz. Está garantizado que cualquier elementoAi,jde la matriz satisface -105 ≤Ai,j≤ 105.
Salida
La salida debe tener exactamente una línea con un sólo número: la máxima suma posible al considerar todas las submatrices no vacías.
Restricciones
Está garantizado que:
- En aproximadamente 30% de los casos,
2 ≤ R, C ≤ 10. - En el resto de los casos,
2 ≤ R, C ≤ 50.
Entrada de ejemplo #1
3 3
2 -1 5
0 8 -3
-6 -4 7
Salida de ejemplo #1
12
Explicación del ejemplo #1
Este es el ejemplo de la imagen.
Entrada de ejemplo #2
2 4
1 2 -3 -4
5 6 -7 -8
Salida de ejemplo #2
14
Explicación del ejemplo #2
En este caso la mejor solución es la submatriz que tiene todos los números positivos y ninguno de los negativos. La suma de esta submatriz es 1 + 2 + 5 + 6 = 14.
Entrada de ejemplo #3
3 2
-3 -2
-4 -5
-7 -6
Salida de ejemplo #3
-2
Explicación del ejemplo #3
Cuando todos los elementos son negativos, la máxima suma también es negativa porque cualquier submatriz tendrá solo números negativos. En este caso, la mejor solución es una submatriz de exactamente un elemento, el elemento menos negativo de todos (-2).
Entrada de ejemplo #4
3 3
1 1 1
1 -1 1
1 1 1
Salida de ejemplo #4
7
Explicación del ejemplo #4
En este caso la mejor solución es la matriz entera. Esta solución incluye el -1 del centro. Vale la pena incluirlo porque esto nos permite agarrar más unos y maximizar la suma total.
Entrada de ejemplo #5
3 3
1 1 1
1 -10 1
1 1 1
Salida de ejemplo #5
3
Explicación del ejemplo #5
Este caso es similar al ejemplo anterior, pero ahora no vale la pena agarrar el número negativo del centro porque es demasiado negativo. La mejor solución ahora es cualquier submatriz que incluya solo unos.
Vale la pena notar que en este caso hay varias soluciones diferentes (básicamente cualquier fila o cualquier columna llena de unos), pero esto no importa porque el problema nos pide imprimir la suma únicamente (no la posición de la submatriz). Es decir, si hay varias soluciones posibles, no hay ambigüedad a la hora de imprimir la salida porque solo queremos la suma.