0x9c - Máximo elemento en un subarreglo enorme

Este problema es casi idéntico al problema 0x9b - Máximo elemento en un subarreglo pequeño. La única diferencia es que ahora el rango de las consultas es mucho más grande lo que hace necesario encontrar una solución más eficiente.

En la avenida principal de Ciudad Codeo hay N edificios numerados de 0 a N-1.

Los edificios podrían tener diferentes alturas (aunque también es posible que haya edificios con exactamente la misma altura). Aquí hay un ejemplo con N = 8. Los números en el eje vertical a la izquierda muestran la altura de los edificios, y los números en la escala horizontal abajo muestran la numeración de los edificios:

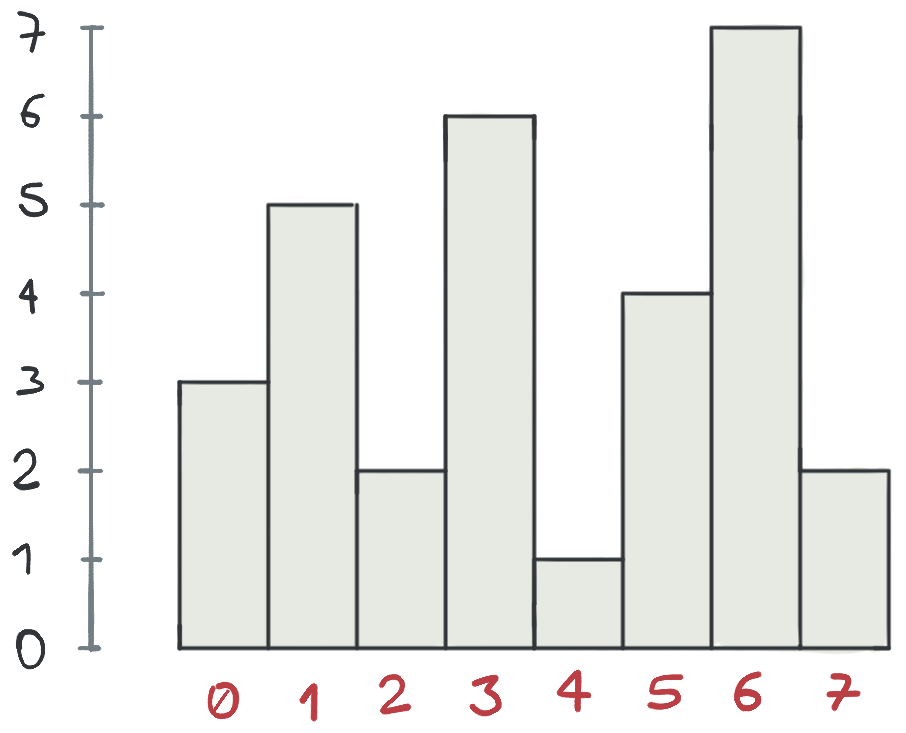
En Ciudad Codeo están grabando una película y para la última escena quieren poner una cámara en el edificio más alto que puedan encontrar, siempre y cuando el edificio no esté demasiado lejos de la acción. Más específicamente, el director de la película escoge un rango de edificios descrito por dos números L y R (que cumplen 0 ≤ L ≤ R < N) y quiere encontrar el edificio más alto entre todos los edificios en ese rango (es decir, el edificio más alto entre todos los edificios cuyo número es mayor o igual a L y menor o igual a R).

Escribe un programa que recibe la altura de todos los edificios y varias consultas (cada una con valores diferentes de L y R). Para cada consulta, tu programa debe encontrar el número del edificio más alto en ese rango.

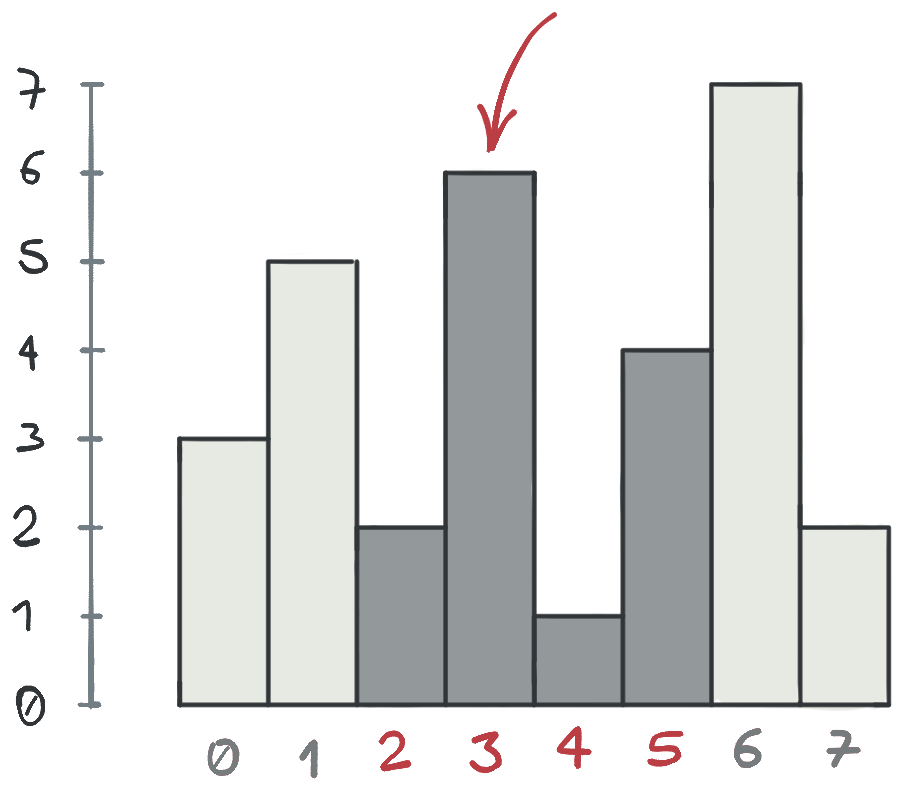
Aquí hay un ejemplo con L = 2 y R = 5. Los edificios 2, 3, 4 y 5 están dentro del rango y se muestran resaltados en la imagen. El edificio más alto entre ellos es el edificio número 3 (que tiene altura 6 y está señalado por una flecha en la imagen):

Entrada

La entrada contiene varias líneas:

• La primera línea contiene N, el número de edificios en la avenida (1 ≤ N ≤ 100,000).
• La segunda línea contiene N enteros Ai para 0 ≤ i < N, la altura de todos los edificios de izquierda a derecha. Estos números están separados por espacios. Está garantizado que Ai satisface 1 ≤ Ai ≤ 109.
• La tercera línea contiene C, el número de consultas (1 ≤ C ≤ 100,000).
• Luego vienen C líneas, cada una con un consulta descrita por dos enteros L y R. Está garantizado que 0 ≤ L ≤ R < N (es decir, L y R son un rango válido que incluye al menos un edificio).

Salida

La salida debe tener exactamente C líneas (una por consulta).

Para cada consulta, escribe el número del edificio más alto dentro del rango.

Si hay varios edificios empatados con la altura máxima dentro del rango, escoge el que está más a la izquierda entre ellos (es decir, el que tiene menor número).

Entrada de ejemplo 1

8
3 5 2 6 1 4 7 2
3
2 5
0 7
4 4

Salida de ejemplo 1

3
6
4

Explicación del ejemplo 1

La entrada nos da los 8 edificios mostrados en la primera imagen más arriba. Luego nos da 3 consultas:

• La primera consulta es L = 2 y R = 5. Este es el ejemplo mostrado en la segunda imagen más arriba. El edificio más alto en este rango es el edificio número 3 que tiene altura 6. La salida es el número de este edificio (3).
• La segunda consulta es L = 0 y R = 7. El rango incluye todos los edificios de la avenida. El edificio más alto de todos es el número 6 (con altura 7).
• La tercera y última consulta es L = 4 y R = 4. Este rango tiene sólo un edificio. El edificio más alto es ese mismo (porque es el único).

Entrada de ejemplo 2

5
1 2 1 2 1
3
0 4
0 2
2 4

Salida de ejemplo 2

1
1
3

Explicación del ejemplo 2

La entrada nos da 5 edificios con alturas [1, 2, 1, 2, 1]. Luego nos da 3 consultas:

• La primera consulta es L = 0 y R = 4 (todos los edificios). En este caso hay dos edificios empatados (el edificio número 1 y el edificio número 3) porque ambos tienen altura 2 (la máxima posible en este caso). La salida debe ser el edificio que está más a la izquierda entre ellos (el edificio 1).
• La segunda consulta es L = 0 y R = 2. En este caso no hay empate porque el edificio 3 no está en el rango.
• La tercera y última consulta es L = 2 y R = 4. En este caso tampoco hay empate.

Envía tu solución