0x99 - Máquina para barajar cartas

¡Felicitaciones! Es tu primer día trabajando como dealer en un casino.

El casino usa una máquina para barajar cartas que funciona de la siguiente manera:

• La máquina tiene N compartimentos numerados de 0 a N-1 de izquierda a derecha. El dealer carga exactamente una carta de la baraja en cada uno de los compartimentos.
• La máquina funciona por rondas. En total, la máquina ejecuta R rondas.
• El resultado de una ronda está determinado por un arreglo P que contiene una permutación de los números del 0 a N-1 (es decir, el arreglo P tiene todos los números del 0 a N-1 en algún orden arbitrario, sin repetir elementos). Después de cada ronda, la carta que estaba en el compartimento i al iniciar la ronda pasa a estar en el compartimiento P[i] al finalizar la ronda.
• La máquina usa el mismo arreglo P para todas las rondas.
• Después de ejecutar todas las rondas, el dealer recolecta todas las cartas de izquierda a derecha.

Veamos un ejemplo con N = 6 y P = [1, 0, 3, 4, 2, 5]. La imagen muestra el proceso al ejecutar 2 rondas:

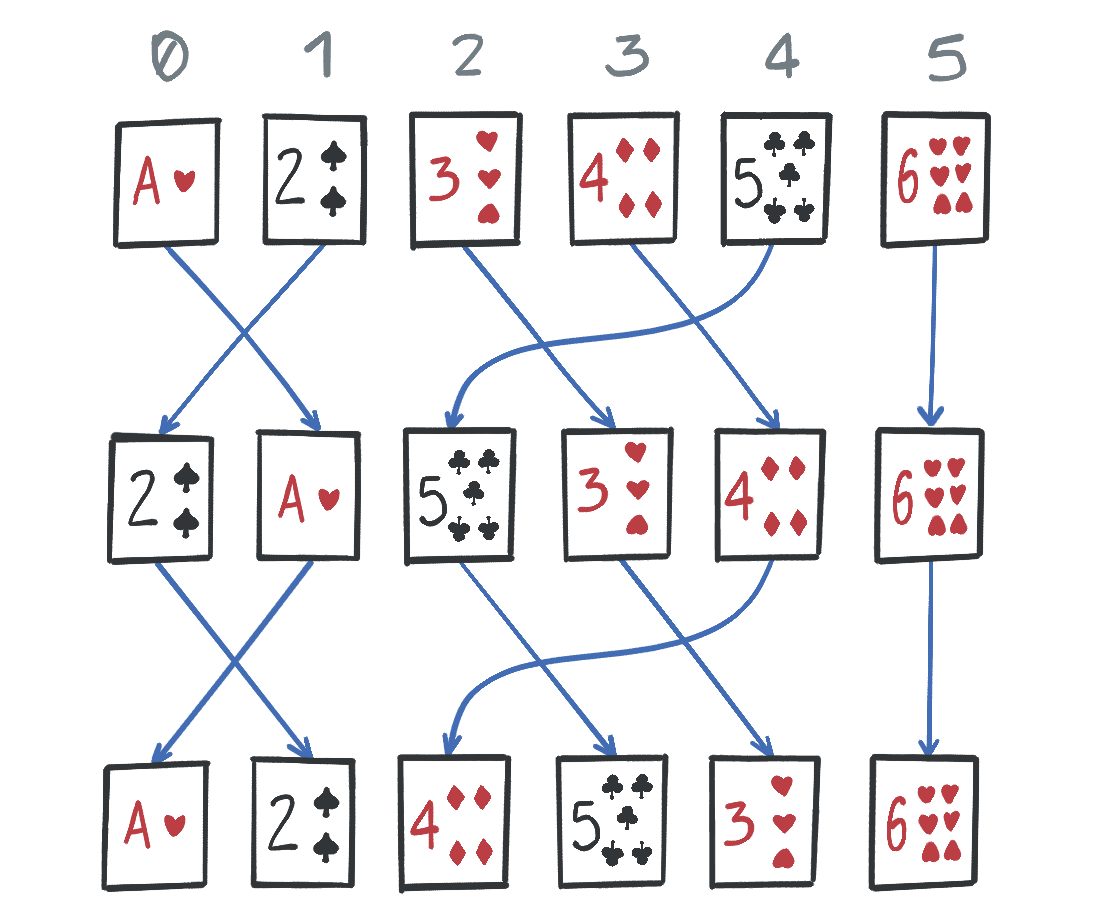
Inicialmente, el dealer carga la máquina con las cartas A♥️, 2♠️, 3♥️, 4♦️, 5♣️ y 6♥️ de izquierda a derecha, como muestra la fila superior. Los números grises arriba muestran el número de cada compartimento.

Las flechas muestran una representación gráfica del arreglo P.

La fila de cartas del medio muestra el resultado después de una ronda, y la fila inferior muestra el resultado después de dos rondas.

Después de una ronda, el A♥️ (que inicialmente está en la posición 0) pasa a estar en la posición P[0] = 1. El 2♠️ (que inicialmente está en la posición 1) pasa a estar en la posición P[1] = 0. El 3♥️ (que inicialmente está en la posición 2) pasa a estar en la posición P[2] = 3) y así sucesivamente.

Después de dos rondas, el A♥️ (que había quedado en la posición 1 después de la primera ronda) pasa ahora a la posición P[1] = 0, el 2♠️ pasa a P[0] = 1, el 3♥️ pasa a P[3] = 4 y así sucesivamente.

Por casualidad, el 6♥️ nunca cambia de posición porque empieza en la posición 5 y P[5] = 5.

Cómo tu eres programador en tu tiempo libre, inmediatamente te das cuenta que esta máquina no es muy segura. Escribe un programa que determina la posición final de cada carta después de un número absurdamente grande de rondas.

Entrada

La entrada contiene varias líneas:

• La primera línea contiene dos enteros N y R. N es el número de compartimentos de la máquina y R es el número de rondas a simular. Está garantizado que 1 ≤ N ≤ 100,000 y 0 ≤ R ≤ 1018.
• La segunda línea contiene el arreglo P. Está garantizado que el arreglo contiene una permutación de los números del 0 a N-1. Los números están separados por espacios.

Por simplicidad, consideramos que todas las cartas son diferentes y están representadas por los números del 1 al N (por ejemplo, el 1 podría representar al A♥️ y el 2 podría representar al 2♠️). Inicialmente el dealer siempre carga las cartas de izquierda a derecha en orden ascendiente: la carta 1 inicia en el compartimento 0, la carta 2 en el compartimento 1 y en general la carta k inicia en el compartimento k-1.

Salida

La salida debe tener exactamente una línea con N enteros separados por espacios: el orden final de las cartas de izquierda a derecha, después de que la máquina ejecuta R rondas.

Entrada de ejemplo 1

6 2
1 0 3 4 2 5

Salida de ejemplo 1

1 2 4 5 3 6

Explicación del ejemplo 1

Este es el ejemplo de la imagen. Nos piden ejecutar 2 rondas con P = [1, 0, 3, 4, 2, 5]:

• Al inicio, el orden de las cartas es [1, 2, 3, 4, 5, 6] (porque el problema nos dice que al inicio siempre cargamos la máquina con los números del 1 al N de izquierda a derecha).
• Después de una ronda, el orden es [2, 1, 5, 3, 4, 6].
• Después de dos rondas, el orden es [1, 2, 4, 5, 3, 6]. Esta es la salida.

Entrada de ejemplo 2

4 1000000000000000000
0 1 2 3

Salida de ejemplo 2

1 2 3 4

Explicación del ejemplo 2

Podríamos decir que esta es una máquina defectuosa. No importa el número de rondas, las cartas nunca se mueven porque en este caso P[i] = i para todo i (es decir, cada carta siempre queda en el mismo compartimento donde ya estaba).

Entrada de ejemplo 3

5 6
1 2 3 4 0

Salida de ejemplo 3

5 1 2 3 4

Explicación del ejemplo 3

Esta máquina hace una "rotación". Después de una ronda, cada carta pasa al compartimento siguiente (y la carta en el último compartimento pasa al primero). En este caso nos piden ejecutar 6 rondas. Este es el proceso:

• Inicialmente, las cartas son [1, 2, 3, 4, 5] (como siempre).
• Después de una ronda el orden es [5, 1, 2, 3, 4].
• Después de dos rondas el orden es [4, 5, 1, 2, 3].
• Después de tres rondas el orden es [3, 4, 5, 1, 2].
• Después de cuatro rondas el orden es [2, 3, 4, 5, 1].
• Después de cinco rondas el orden es [1, 2, 3, 4, 5].
• Después de seis rondas el orden es [5, 1, 2, 3, 4]. Esta es la salida.

Entrada de ejemplo 4

3 0
0 2 1

Salida de ejemplo 4

1 2 3

Explicación del ejemplo 4

En este caso nos piden ejecutar 0 rondas, entonces la salida es simplemente el orden inicial de las cartas.

Envía tu solución