0x94 - Subarreglo de máxima suma

Tenemos un arreglo de enteros llamado A. Un subarreglo es un bloque de elementos consecutivos de elementos de A.

Por ejemplo, si A = [-3, 5, -1, 2], estos son algunos de sus subarreglos:

• [-3]
• [5, -1]
• [-3, 5, -1, 2]

Decimos que la suma de un subarreglo es la suma de todos sus elementos. Escribe un programa que encuentre el subarreglo de A cuya suma sea lo más grande posible.

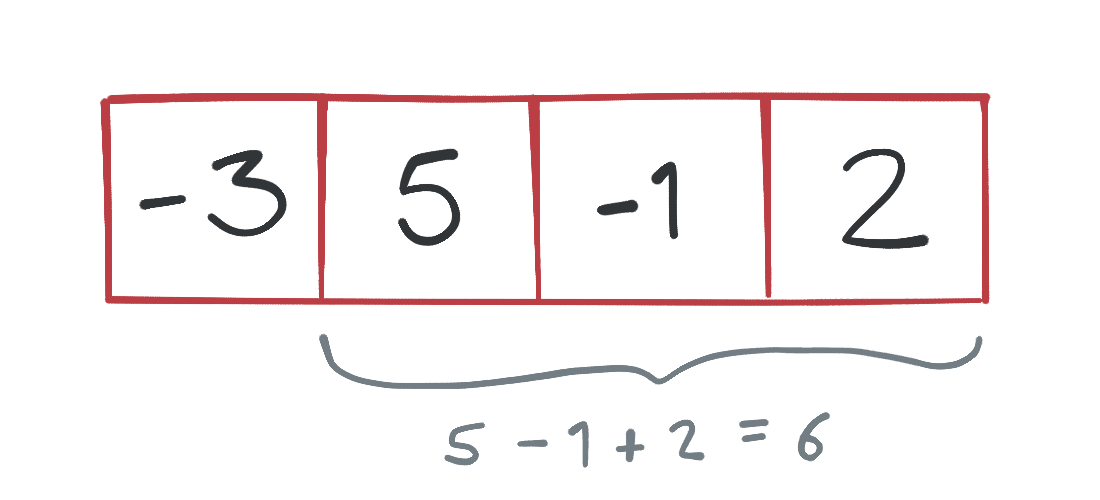
En nuestro ejemplo, la respuesta es el subarreglo [5, -1, 2] que tiene suma 6. Todos los demás subarreglos tiene una suma menor:

Entrada

La entrada contiene varias líneas:

• La primera línea contiene N, el número de elementos en el arreglo.
• La segunda línea contiene N enteros Ai para 0 ≤ i < N, los elementos del arreglo. Estos números están separados por espacios. Está garantizado que Ai satisface -10⁹ ≤ Ai ≤ 10⁹.

Salida

La salida debe tener una única línea con un entero, la máxima suma posible entre todos los subarreglos de A.

Sólo debes considerar subarreglos que tienen por lo menos un elemento (en otras palabras, no es válido considerar un subarreglo vacío).

Entrada de ejemplo #1

4
-3 5 -1 2

Salida de ejemplo #1

6

Explicación del ejemplo #1

Este es el ejemplo del principio. [5, -1, 2] es el subarreglo de máxima suma y su suma es 6. Cualquier otro subarreglo tiene suma menor a 6.

Entrada de ejemplo #2

4
-1 -3 -2 -4

Salida de ejemplo #2

-1

Explicación del ejemplo #2

Cuando todos los elementos son negativos, no vale la pena agarrar 2 o más elementos. Entonces la respuesta es un subarreglo con un único elemento, el elemento menos negativo de todos.

Entrada de ejemplo #3

3
0 0 0

Salida de ejemplo #3

0

Explicación del ejemplo #3

Cuando todos los elementos son 0, todos los subarreglos tienen suma 0.

Entrada de ejemplo #4

3
10 -1 10

Salida de ejemplo #4

19

Explicación del ejemplo #4

La mejor respuesta es agarrar todos los elementos. Vale la pena incluir el -1 porque nos permite agarrar los dos dieces y maximizar la suma.

Entrada de ejemplo #5

3
10 -100 10

Salida de ejemplo #5

10

Explicación del ejemplo #5

Ahora no vale la pena incluir el elemento negativo del medio, porque es demasiado negativo.

Restricciones

• Está garantizado que 1 ≤ N ≤ 80,000.

Pistas

Este problema tiene varias soluciones con varias complejidades: O(n2) , O(n log n) y por lo menos dos soluciones O(n) diferentes. ¿Puedes encontrarlas todas?

Envía tu solución