0x53 - Encontrar ciclos en un grafo dirigido

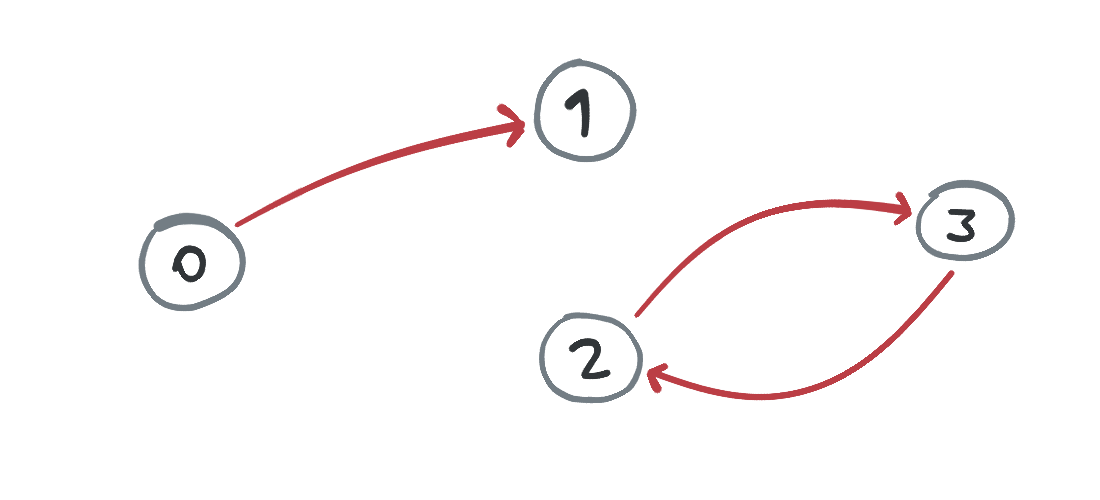
Un grafo dirigido es un grafo en el que las aristas sólo pueden recorrerse en una dirección. Gráficamente se usan flechas para mostrar la dirección de las aristas. Por ejemplo:

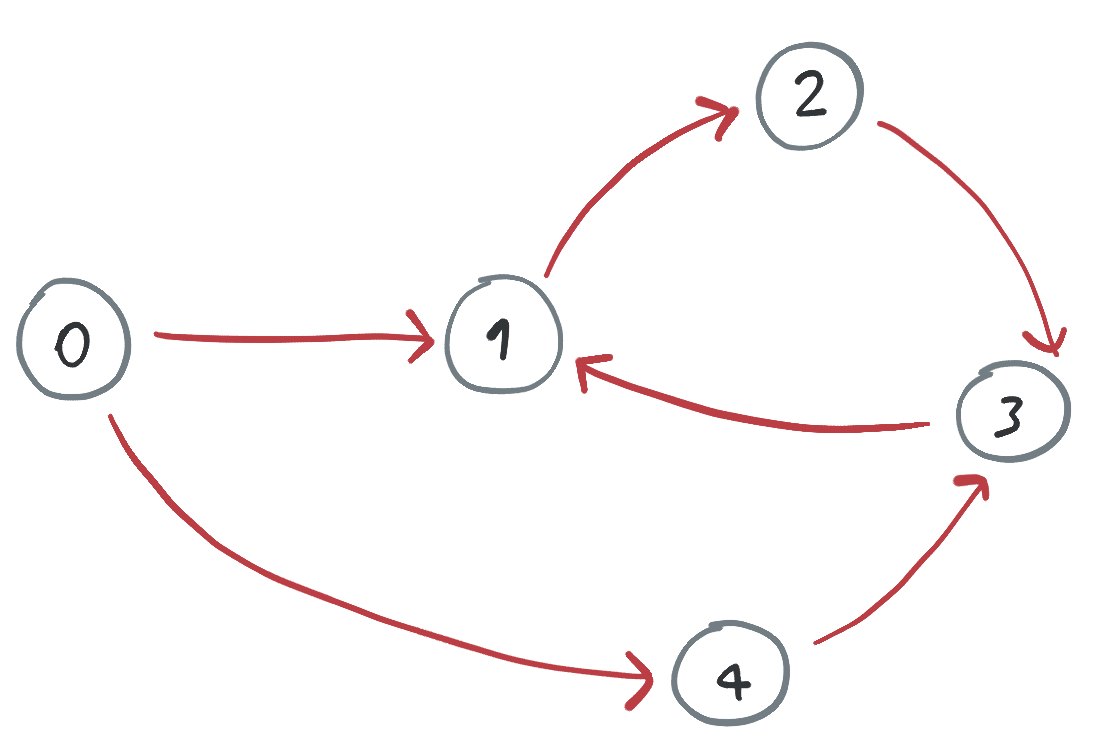
Un ciclo es un camino en el grafo en el que se inicia en algún nodo y se regresa a él después de recorrer una o más aristas (respetando su dirección). En el grafo anterior hay un ciclo usando los nodos 1, 2 y 3:

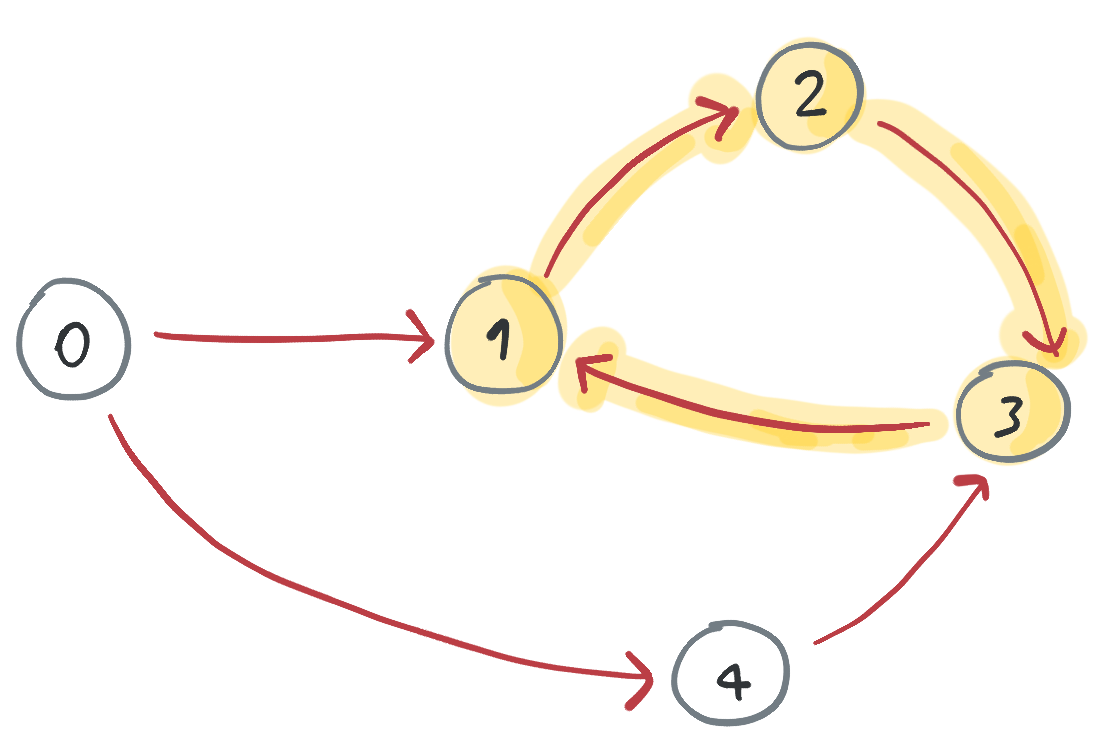
No todos los grafos dirigidos tienen ciclos. Por ejemplo, si cambiamos la dirección de la arista que va de 1 a 3 en el grafo anterior por casualidad quedamos con un grafo sin ciclos:

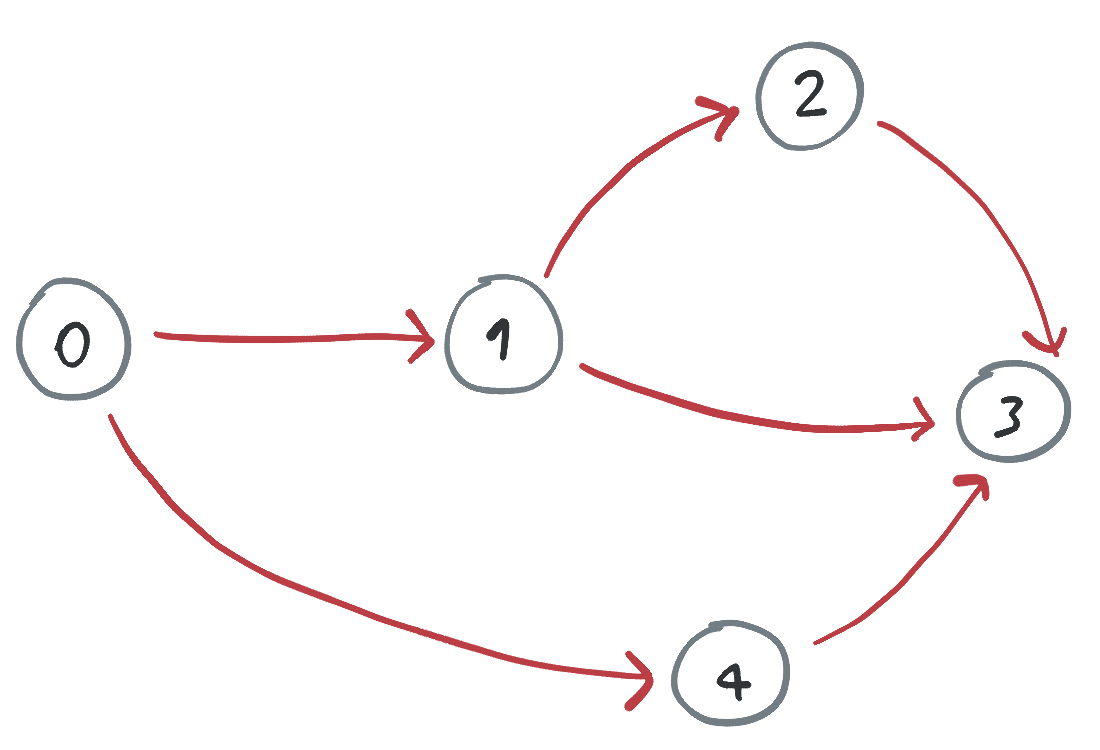
Escribe un programa que recibe un grafo dirigido y determina si existe algún ciclo o no.

Entrada

La entrada contiene varias líneas:

• La primera línea contiene dos enteros N y M.
  • N es el número de nodos en el grafo. Los nodos están numerados de 0 a N-1. Está garantizado que 1 ≤ N ≤ 10,000.
  • M es el número de aristas en el grafo. Está garantizado que 0 ≤ M ≤ 50,000.
• Luego vienen M líneas (una por arista), cada una con dos enteros ui y vi para 0 ≤ i < M, indicando que hay una arista desde el nodo ui hacia el nodo vi.
  • Está garantizado que 0 ≤ ui, vi < N (es decir, las aristas empiezan y terminan en nodos válidos).
  • Es posible que haya aristas duplicadas.
  • Es posible que ui == vi (es decir, es posible que haya una arista de un nodo a él mismo).

Salida

La salida debe tener exactamente una línea con la palabra Yes si el grafo dirigido contiene por lo menos un ciclo o No en caso contrario.

Entrada de ejemplo #1

5 6
0 1
0 4
1 2
2 3
3 1
4 3

Salida de ejemplo #1

Yes

Explicación del ejemplo #1

Este es el grafo de la primera imagen. Hay un ciclo entre los nodos 1, 2 y 3.

Entrada de ejemplo #2

5 6
0 1
0 4
1 2
1 3
2 3
4 3

Salida de ejemplo #2

No

Explicación del ejemplo #2

Este es el mismo grafo del ejemplo #1 pero cambiamos la dirección de la arista que va de 1 a 3. Ahora no hay ciclos.

Entrada de ejemplo #3

3 0

Salida de ejemplo #3

No

Explicación del ejemplo #3

Este es un grafo en el que no hay ninguna arista:

Si no hay ninguna arista tampoco puede haber un ciclo, porque por definición un ciclo es un camino que inicia y termina en el mismo nodo y utiliza por lo menos una arista.

Entrada de ejemplo #4

1 1
0 0

Salida de ejemplo #4

Yes

Explicación del ejemplo #4

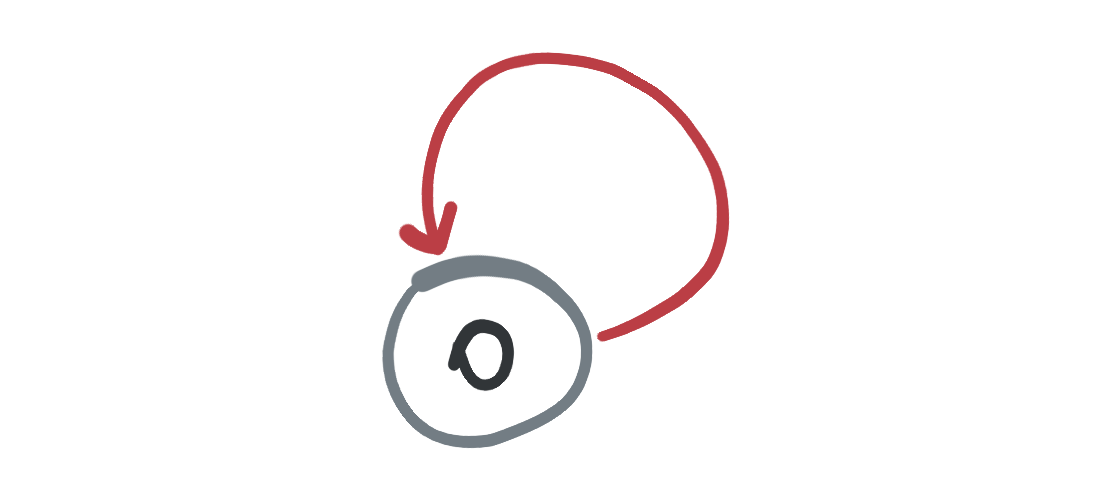
Este es un grafo en el que hay un sólo nodo pero hay un ciclo porque se puede recorrer al menos una arista empezando en el nodo 0 y terminando en el nodo 0:

Entrada de ejemplo #5

4 6
0 1
0 1
0 2
0 2
1 3
2 3

Salida de ejemplo #5

No

Explicación del ejemplo #5

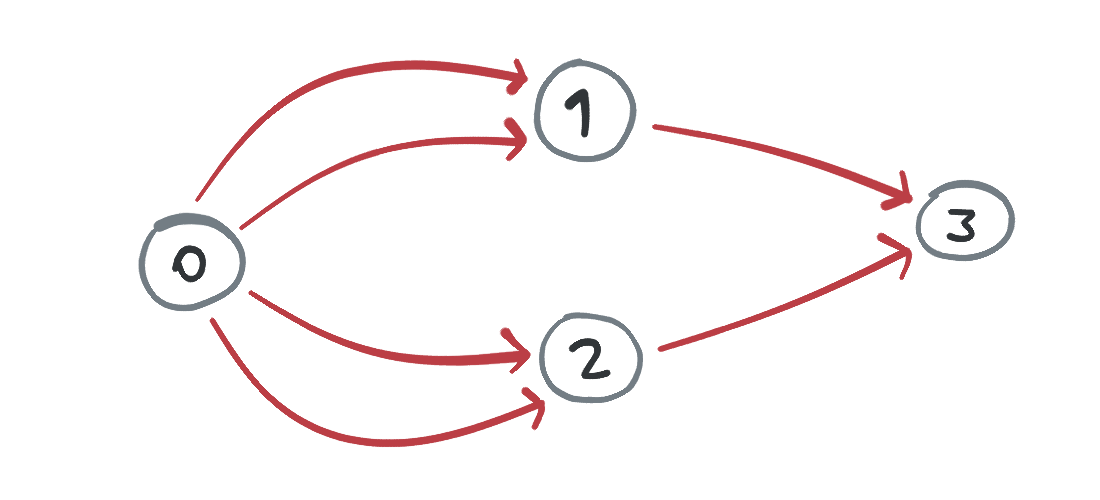
En este grafo hay aristas duplicadas, pero aún así no hay ningún ciclo:

Entrada de ejemplo #6

4 3
0 1
2 3
3 2

Salida de ejemplo #6

Yes

Explicación del ejemplo #6

Este es un grafo en el que no todos los nodos están conectados. Aún así, hay un ciclo entre los nodos 2 y 3:

Envía tu solución